A Markov Chain is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event.

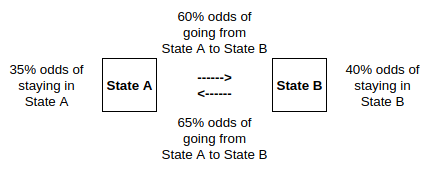
From Wikipedia: A diagram representing a two-state Markov process, with the states labelled E and A. Each number represents the probability of the Markov process changing from one state to another state, with the direction indicated by the arrow. For example, if the Markov process is in state A, then the probability it changes to state E is 0.4, while the probability it remains in state A is 0.6.

• Let $s_t$ be a random variable taking values in ${1,2,…,N}$
• Let $a_{i,j} = \mathbb{P}(s_t=j \mid s_{t-1}=i)$ denote the transition probability from state i to state j
• $s_t$ is a Markov Chain if $\mathbb{P}(s_t=j\mid fs_{t-1}=i, s_{t-2=k,…}) = \mathbb{P}(s_t=j\mid s_{t-1}=i) = a_{i,j}$

The state dynamics are fully specified by:

\[A = \begin{bmatrix} a_{1,1} & ... & a_{1,N} \\ a_{i,1} & ... & a_{i,N} \\ a_{N,1} & ... & a_{N,N} \end{bmatrix}\]

Since $\sum_{j}\mathbb{P}(s_t=j \mid s_{t-1=i})$, the elements of each row add up to unity:

\[a_{i,1} + ... + a_{i,N} = 1\]

Let $e_i$ denote the i-th row vector of the N x N identity matrix. Let $\xi_t$ denote a 1 x N row vector that is equal to $e_i$ when the state $s_t$ is equal to i:

\[\xi_t = (0, ..., 0, 1_{i^{th}\\ element}, 0, ..., 1)\]

The expectation of $\xi_{t+1}$ is a vector whose j-th element is the probability that $s_{t+1} = j$:

\[\mathbb{E}(\xi_{t+1} \mid s=i)=(a_{i,1}, ..., a_{i,N})\]

We infer that $\mathbb{E}(\xi_{t+1} \mid s_t=1) = \xi_t\bf{A}$, or more generally that $\mathbb{E}(\xi_{t+1}\mid \xi_{t}) = \xi_t\bf{A}$ and since $s_t$ follows a Markov Chain:

\[\mathbb{E}(\xi_{t+1} \mid \xi_{1}, ..., \xi_t) = \xi_t\bf{A}\]

In summary this means that when $s_t$ is i, then $\xi_t$ will represent a row-vector of the identity matrix which corresponds to the relevant transition probability. And when multiplied by the transition matrix gives you the transition probability. But of course, as Markov Chains only depend on the most recent state, the expectation of the next period’s $\xi$ value $\xi_{t+1}$ is simply equal to the current $\xi_t$ value times the transition matrix. It’s essentially like an over-complicated lookup function.

Two-Step Transition Probabilities

The probability that $s_{t+2}=j$ given $s_t=1$ by:

\[\mathbb{P}(s_{t+2}=j \mid s_t=i)=a_{i,1}a_{1,j}+...+a_{i,N}a_{N,j}\]

which can also be recognized as the i-th row and j-th column element of the transition matrix squared $\bf{A}^2$. The odds of two things happening one after the other is simply the odds squared, which is what we are saying here.

N-Step Transition Probabilities

In general, the probability that $s_{t+m}=j$ given $s_t=i$ is given by the row j, column i element of $\bf{A}^m$:

\[\mathbb{E}(\xi_{t+m} \mid \xi_t, \xi_{t-1}, ..., \xi_1) = \xi_t \bf{A}^m\]

Ultimately we are locating the appropriate probability in the transition matrix and raising it to the nth power depending on how many steps forwards we are going.

Forecasting Transitions

Assume that we have received some information $I_t$ up to date $t$. Let

\[\pi_t = [\mathbb{P}(s_t=1 \mid I_t), ..., \mathbb{P}(s_t=N \mid I_t)]\]

denote the conditional probability distribution over the state space. What is out best forecast of $s_{t+1}$ given $I_t$? Since $\pi_t = \mathbb{E}(\xi_t \mid I_t)$, we infer that

\[\pi_{t+1} = \mathbb{E}(\xi_{t+1}|I_t) = \mathbb{E}(\xi_t \mid I_t)\bf{A}\]

If $I_t$ contains no leading information then $\mathbb{E}(\nu_{t+1} \mid I_t)=0$. The forecast state distribution is therefore

\[\pi_{t+1} = \pi_t\bf{A}\]

This essentially means that the 1-step forward conditional probability distribution $\pi_{t+1}$ is equal to the current probability distribution $\bf{A}$ multiplied by the current period transition matrix $\pi_t$. The current probability distribution $\pi_t$ already includes all the information up until t.

Stationary Distributions

To make note of something related to Forecasting Transitions; a distribution $\pi$ is stationary if it satisfies $\pi = \pi\bf{A}$, which means that today’s forecast distribution $\pi$ is the same as today’s distribution $\bf{A}$. If the Markov Chain is ergodic, then the system

\[\begin{align} \pi &= \pi\bf{A} \\ \pi\iota &= 1 \end{align}\]

has a unique solution. Here $\iota$ denotes the $(N \times 1)$ vector with all elements equal to unity.